Paradoxes d’Achille et la tortue : Réfutation de la prétendue résolution mathématique
Version 12 du 20.7.2024
Présentation du paradoxe sous un nouvel éclairage en forme de puzzle :
Le paradoxe d'Achille et de la tortue, du philosophe grec Zénon, illustre une situation où Achille, un coureur rapide, donne une avance de 100 mètres à une tortue lente. Lorsque Achille court après la tortue, il doit d'abord atteindre le point où la tortue se trouvait initialement à 100m ce qui lui prend un certain temps et un certain parcours. Mais une fois ce point atteint, il s'aperçoit que pendant son propre parcours, sa rivale a avancé un peu plus loin et est désormais plus loin. Achille doit alors atteindre ce nouveau point, et ainsi de suite, en une suite de distances de plus en plus petites sans fin, ce qui crée une série infinie de nouvelles distances à parcourir.
Bien que ces distances restantes se réduisent sans fin, cette série de distances à parcourir peut être comparée à un puzzle d’espace et de temps avec un nombre infini de pièces, qu'il faut ajouter incessamment dans un ordre précis : « A », « B », « C », etc. Mais puisque le nombre de ces nouveaux termes est infini, il semble que ce puzzle ne pourra jamais être finalisé par une dernière pièce. Pourtant, les faits montre qu’Achille finit par dépasser sa concurrente d’où le paradoxe.
Ma divergence avec l’idée de Zénon :
Là où Zénon prétendait que le dépassement n’aurait jamais lieu, je penses plus utile de reconnaître la réalité de ce dépassement puisqu’il fait partie d’un fait non contestable et avéré. Il ne s’agit donc plus de nier le celui-ci mais d’expliquer pourquoi il survient malgré cela. Ce ne sera que lorsque nous expliquerons comment le puzzle de la course peut être terminé dans la chronologie infinie que nous pourrons prétendre avoir résolu le problème.
Réfutation de la résolution mathématique
De nos jours, beaucoup considèrent que ce paradoxe de Zénon a été résolu grâce au calcul infinitésimal. Cette idée est répandue sur des plateformes comme Wikipédia et dans quelques articles et vidéos, donnant l’impression que le paradoxe est définitivement clos.
L'argument semble simple : en sommant l'ensemble des parcours ajoutés, le calcul infinitésimal permet de déterminer qu’Achille dépassera sa rivale à un moment précis.
Le raisonnement se targue en ces termes : si l’on peut calculer précisément où Achille dépassera la tortue, c’est nécessairement que Zénon se trompe en affirmant qu’Achille ne dépassera jamais sa rivale.
En quoi la solution proposée ne réfute pas Zénon ?
Le graphique suivant de Wikipédia tente de reproduire le paradoxe de Zénon sans problème apparent.

En considérant les vitesses respectives de 10 m/s pour Achille et 5 m/s pour la tortue, avec une avance initiale de 100 mètres, le calcul divise le temps en deux parties égales à chaque nouvelle étape franchie par Achille, ce qui est normal puisque la tortue avance deux fois moins vite. Cela conduit à la conclusion qu’Achille rattrapera la tortue après 20 secondes. Si ce graphique est juste et que le calcul infinitésimal permet effectivement de calculer le moment du dépassement, il n’explique rien de plus que ce que tout un chacun sait sans recourir à des calculs : le dépassement après 20 secondes… rien de plus.
Sans dépassement, plus de paradoxe : pourquoi constater le dépassement ne suffit pas à résoudre l’énigme ?
Un paradoxe apparaît lorsque deux observations avérées et indéniablement vérifiables empiriquement se contredisent.
Premièrement : Achille finit par rattraper la tortue, un fait évident qui ne nécessite aucune analyse mathématique et qui semble logique si on considère la différence de vitesse.
Deuxièmement : Si à chaque fois qu’Achille atteint une position antérieure de la tortue, celle-ci s’est déjà déplacée un peu plus loin. Peut-on nier cela ? Évidemment que non…
Ce dernier constat, tout aussi pertinent que le dépassement, s’oppose à celui-ci.
Ainsi, calculer le moment où Achille dépasse sa rivale ne fait que mettre à jour le paradoxe, au lieu de le réfuter.
L’observation de Zénon n’est pas une simple fantaisie que l’on peut balayer du revers de la main.
Le problème est qu’aucune de ces deux assertions n'est plus réfutable que l’autre, et pourtant elles se contredisent, faisant apparaître l’immense paradoxe.
Nier Zénon mène à la téléportation
Nier qu’Achille doive passer par ces positions antérieures avant de dépasser sa rivale reviendrait à dire qu’Achille pourrait éviter ces positions intermédiaires. Cela impliquerait de passer d’un point de la course directement au dépassement de la tortue sans franchir ces itinéraires intermédiaires, ce qui ne pourrait être possible que par une téléportation. Si on refuse de reconnaître que chaque fois qu'Achille atteint une position antérieure de la tortue, celle-ci a avancé, alors on serait contraint de supposer que la tortue peut se déplacer instantanément d'un point à un autre, sans parcourir les distances intermédiaires. Cette hypothèse de téléportation contredit non seulement l'expérience empirique du mouvement continu mais introduit également une notion incohérente avec la réalité physique.
Contredire Zénon n’est donc pas une tâche facile. Affirmer simplement qu’il a tort juste parce que le dépassement est constaté non seulement n’est pas valable puisque ce dépassement est au cœur du paradoxe mais de plus, ce rejet va à l’encontre de l’observation que la tortue a avancé pendant qu’Achille atteignait sa dernière position, une observation qui est confirmée par l’expérience empirique. Ce serait donc contredire le mouvement lui-même. Cela mène à des conclusions absurdes, comme celle de la téléportation.
L’erreur de l’idée des distances négligeables
Une autre erreur serait de penser que les distances deviennent si petites qu’elles en seraient négligeables. C’est en effet une erreur courante que l'on trouve sur Internet, car négliger des distances parcourues, aussi petites soient-elles, équivaut à prétendre que le puzzle serait fini alors qu’il lui manque une infinité de petites pièces, jugées négligeables uniquement parce qu’elles sont microscopiques. C’est un faux raisonnement également.
Or, si on enlève ne serait-ce qu'une seule de ces infimes petites distances, alors le parcours ne serait plus traversé dans sa totalité et le mouvement ne serait pas complet. Pour qu’Achille puisse atteindre sa rivale, il n’est pas possible de penser ainsi ; les mouvements négligeables n’existent pas.
La limite et la convergence : deux notions à distinguer qui reproduisent l’idée de Zénon :
Pour comprendre le paradoxe d’Achille et la tortue, par le calcule infinitesimal il ne suffit pas de constater le dépassement mais il est essentiel de distinguer entre les concepts de deux concepts : la limite et de convergence, car ces deux notions, bien que liées, abordent le problème sous des angles différents et reproduisent l’idée de Zénon.
La limite, dans ce contexte, représente le parcours total une fois celui-ci terminé. Si l’on considère la distance totale que doit parcourir Achille pour rattraper la tortue comme un puzzle, la limite en est l’image finale : même si le puzzle est une division infinie du mouvement, cette division ne rend pas la distance plus grande. Mathématiquement, la somme infinie des distances de plus en plus petites (10 mètres, puis 1 mètre, puis 0,1 mètre, etc.) aboutit à une valeur finie, démontrant qu’Achille finit par atteindre la tortue. Cependant, cette approche ne tient pas compte du temps écoulé pour chaque segment du parcours.
La convergence, en revanche, s’intéresse à la dynamique temporelle du mouvement. Elle pose la question de comment finir ce puzzle dans l’épreuve du temps. Chaque fois qu’Achille atteint une position antérieure de la tortue, celle-ci s’est déplacée un peu plus loin. La convergence décrit ce processus de rapprochement continu, où chaque étape est une fraction de plus en plus petite de la distance restante. Mais cette série de déplacements ne cesse jamais véritablement, car à chaque nouvelle position atteinte par Achille, il y a toujours une nouvelle position, bien que plus petite, à atteindre. C’est pourquoi on ne dit pas que ces valeurs atteignent la tortue mais qu’elles convergent.
Cela illustre parfaitement l’idée de Zénon : il y a toujours une distance supplémentaire à franchir, si petite soit-elle, et ainsi le mouvement semble ne jamais pouvoir être achevé .
Ainsi, si l’on regarde la limite intemporelle, on peut conclure qu’Achille rattrapera la tortue. Cependant, si l’on considère la convergence, on en arrive à la conclusion inverse. C’est pourquoi, dans le calcul infinitésimal proposé sur Wikipedia, limite et convergence reproduisent fidèlement le paradoxe. D’une part, la limite montre que la somme des distances, bien que infinie, est finie et que le dépassement a lieu. D’autre part, la convergence montre que le processus de rattrapage est sans fin, car il y a toujours une nouvelle distance, aussi petite soit-elle, à parcourir ce qui pose la question de comment finir ce puzzle sans pièces final.
On pourrait dire que parce que la convergence mène à la limite, cela suggère que la convergence est égale à la limite, ce qui est vrai et faux en même temps. C’est vrai dans le sens où la convergence montre que les distances se rapprochent indéfiniment de la limite. Cependant, c’est faux dans le sens où la convergence implique un processus continu et jamais totalement achevé, alors que la limite représente un état final, achevé. Cette dualité est au cœur du paradoxe de Zénon, où le mouvement semble à la fois se compléter et rester perpétuellement en cours.
Il ne suffit donc pas de prendre en considération uniquement la limite ou uniquement la convergence, car les deux processus sont inhérents au mouvement. Nier l’un ou l’autre mène à des conclusions absurdes. Si on ne traite que la limite pour affirmer qu’elle concorde avec l’observation du dépassement, on néglige l’observation de la convergence, qui reproduit fidèlement le fait que la tortue continue de se déplacer pendant qu’Achille tente de la rattraper. Un fait tout aussi indéniable, et nier cela revient à supposer une forme de téléportation, ce qui contredit notre expérience empirique du mouvement.
La convergence : placer les pièces du puzzle dans un ordre précis
L'erreur commune serait de penser que, puisque le dépassement est effectif par l'observation, on pourrait rejeter la convergence pour ne traiter que la limite, mais c'est une erreur. Car, dans le temps, seule la convergence est capable de reproduire fidèlement l'épreuve du temps. Se contenter de calculer la limite pour présenter l'état du puzzle fini, c’est oublier d’expliquer comment cela s’est fait dans la progression temporelle où le parcours d’Achille doit passer dans un ordre chronologique d’étapes sans en altérer l’ordre, « A », « B », « C », etc., à l’infini. Ignorer une seule de ces étapes serait comme prétendre que le puzzle serait fini car les pièces manquantes seraient si petites qu’elles pourraient être négligeables. Or, si des pièces manquent, alors la finalité du mouvement n’est plus réalisable.
La limite n'explique pas comment le puzzle peut être finalisé sans dernière pièce ni avec un nombre infini de pièces. Elle ne fait que constater le dépassement, sans l’expliquer. Ainsi, loin de résoudre le paradoxe, le calcul infinitésimal le reproduit fidèlement avec beaucoup d’élégance. D'une part, la convergence pose la question de comment la limite peut être atteinte et, d'autre part, sans dernière pièce au puzzle, elle s’oppose directement à l’atteinte de cette limite. Bien que la convergence permette de situer où doit se trouver la limite, ni la convergence ni la limite ne peuvent expliquer comment le puzzle peut être finalisé. Aucun de ces deux principes ne résout l’intrigue millénaire de Zénon.
La limite indique où le puzzle sera fini, mais la convergence montre que l'atteinte de cette limite n'est mathématiquement pas réalisable. Voilà pourquoi il est incorrect de croire que le calcul infinitésimal pourrait résoudre l'équation ; c’est un paralogisme où seule la limite a été prise en compte et la convergence simplement omise. Or, c’est bien par la convergence que le paradoxe de Zénon prend tout son sens et sa force. En oubliant cette donnée essentielle du problème, on constate uniquement un dépassement, ce qui ne réfute aucunement Zénon, bien au contraire.
L'exploration du paradoxe à travers l'analogie du puzzle nous enseigne que la question véritable n'est pas de savoir si Achille dépasse la tortue, puisqu'elle est dépassée ; le paradoxe naît précisément de ce dépassement et de cette finitude calculée par la limite. Il s’agit plutôt d’être en mesure d’expliquer comment ce dépassement est rendu possible sans dernière pièce au puzzle, ce que ni la limite ni la convergence ne sont en mesure d’expliquer.
L’erreur de confondre une série géométrique d’une série convergente
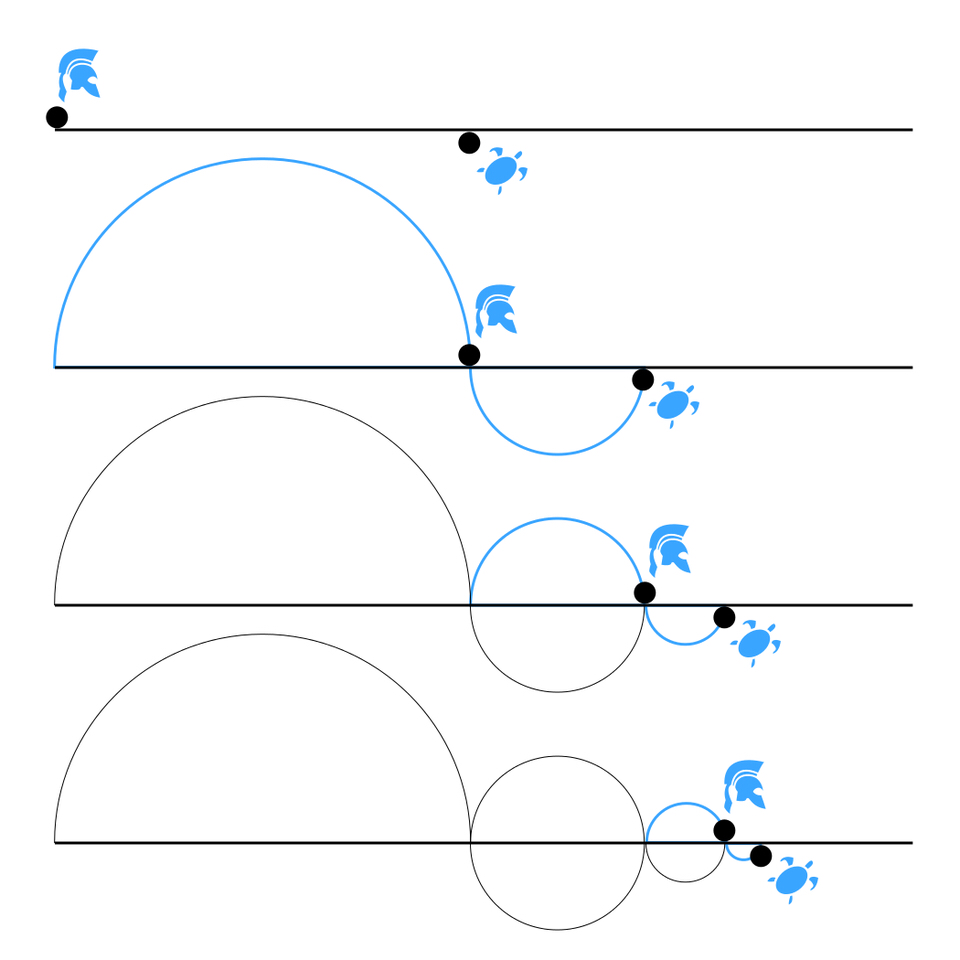
Lorsque l'on entend dire sur Wikipedia que le paradoxe est résolu en utilisant le fait qu'une série infinie de nombres strictement positifs peut converger vers un résultat fini, l’erreur ici est de confondre la convergence et le résultat fini de la limite, puisque ce sont deux choses distinctes comme nous venons de le voir. C’est un peu comme si on considérait le problème de ce parcours comme s’il était un espace statique divisé à l’infini en petits morceaux, à l’exemple d’une série géométrique. Une série géométrique est une suite de termes où chaque terme est obtenu en prenant une fraction constante du terme précédent. Par exemple, si l’on commence avec une quantité entière et que chaque partie suivante est la moitié de la précédente (1, 1/2, 1/4, 1/8, …), cela forme une série géométrique. On peut visualiser cela comme un puzzle comportant une infinité de subdivisions internes : même s’il est composé d’un nombre infini de pièces, il ne deviendra pas plus grand qu’il ne l’est. L’agrégation de toutes les pièces donnera toujours la même surface à ce puzzle.
Exemple sur ce schéma :

Cependant, cette vision statique néglige le facteur temps et l’aspect dynamique du parcours d’Achille et de la tortue. Chaque segment de la série doit être parcouru successivement dans le temps, ce qui signifie qu'Achille doit atteindre chaque position intermédiaire avant de dépasser la tortue. Contrairement à une simple agrégation spatiale des pièces d'un puzzle, qui peut se faire instantanément dans l'esprit, le parcours d’Achille est un processus dynamique nécessitant du temps pour que chaque segment soit franchi.
Cette différence est cruciale car elle souligne que le paradoxe de Zénon n’est pas seulement une question de division infinie de l’espace, mais aussi de la réalisation de ces divisions dans le temps. La série convergente, qui représente les positions successives d'Achille, se construit progressivement dans le temps. Chaque fraction de distance à parcourir est associée à une fraction de temps, et c’est ce passage chronologique à travers ces segments qui crée le paradoxe.
Ainsi, bien que mathématiquement la somme des segments puisse converger vers une distance finie (comme dans le cas de la série géométrique), le fait que chaque segment doive être parcouru chronologiquement implique un processus continu et dynamique.
C’est lorsqu'on cherche à comprendre comment cette série convergente se finalise dans le temps que le paradoxe apparaît. Si on néglige l’ordre chronologique des termes d’espace restant à parcourir, ajoutés en une infinité de nouveaux termes dans l’épreuve du temps, on peut faussement conclure que la somme totale des termes, égale à la limite, signifie que la série convergente est elle-même finie.
Mais c’est une erreur, comme nous l’avons vu, il ne faut pas confondre la convergence et la limite, qui, contrairement à la convergence, est intemporelle. En mathématiques, le fait que la série converge vers une valeur fixe n’enlève rien à la nature convergente de la série, dont la spécificité est de se rapprocher indéfiniment de la limite sans jamais la dépasser. Le passage successif à travers un nombre infini de nouveaux segments dans l’espace-temps est ce qu'il faut expliquer. Comment est-ce possible de finaliser une série convergente sans pièce finale au puzzle ?
L’erreur de l’idée des distances négligeables
Une autre erreur serait de penser que les distances deviennent si petites qu’elles en seraient négligeables. C’est en effet une erreur, car négliger des distances parcourues, aussi petites soient-elles, équivaut à prétendre que le puzzle serait fini alors qu’il lui manque une infinité de petites pièces microscopiques. Or, si on enlève ne serait-ce qu'une seule de ces infimes petites distances, alors le parcours ne serait plus traversé dans sa totalité et le mouvement ne serait pas complet. Pour qu’Achille puisse atteindre sa rivale, il n’est pas possible de penser ainsi. Il n’existe pas de mouvement négligeable.
Téléportation quantique
Comme je l’ai dit, nier le principe de la convergence en ne considérant que la limite pour affirmer que la pierre atteint l’arbre reviendrait à supposer qu’un mobile pourrait passer directement de son point de départ à son arrivée.
Pourrions-nous alors envisager l’hypothèse que cette téléportation pourrait être une réalité dans l’infiniment petit en physique quantique ?
C’est effectivement une idée intéressante, mais elle n’est pas prouvée. Même si une telle téléportation quantique était confirmée un jour, elle ne résoudrait pas le paradoxe car elle soulèverait d’autres paradoxes. C’est une autre proposition d’explication que j’aborde dans un article connexe.
Recherche personnel :
Dans ma jeunesse en 1998, j’ai redécouvert par hasard le paradoxe de dichotomie de Zénon sans avoir jamais entendu parler des paradoxes de Zénon. Cela m’a conduit, au fil des décennies, à développer une pensée indépendante de ce qui avait été exploré auparavant par d’autres penseurs. En tentant de l’expliquer, j'ai élaboré plusieurs théories spatio-temporelles dans lesquelles je me demande si le temps pourrait être une sorte d’hologramme, une illusion de notre propre esprit. Bien que mes idées actuelles ne soient que des spéculations et que je reconnaisse les lacunes de mes propres théories qui nécessitent encore d'être comblées, je partage le cheminement de mes réflexions approfondies accumulées au fil des décennies de travail, expliquant pourquoi ces concepts me semblent assez pertinents.
Je propose que l’univers s’étend au-delà des quatre dimensions perceptibles, avec l’infini comme cinquième dimension de l’univers et l’éternité comme la sixième. Dans cette nouvelle cosmologie d’un cosmos à 6 dimensions, je suggère que sans la compréhension de ces dimensions supplémentaires, il serait peut-être logique de percevoir des contradictions dans les paradoxes de Zénon. Selon ces hypothèses, ces contradictions apparaîtraient car nos sens ne nous permettent pas de saisir la réalité de ces dimensions supérieures. Ne percevant l’univers qu’en 4D, nous sommes peut-être démunis pour résoudre les paradoxes millénaires de Zénon.
Mon livre numérique gratuit sur mon site explore ces concepts nouveaux et propose des réponses possibles à ces énigmes. Vous pouvez découvrir ces idées dans le premier chapitre intitulé :
Les chapitres suivants de mon livre vont bien au-delà du simple cadre des problèmes de Zénon et présentent des théories qui, tout comme celles de Zénon, s’appuient sur des faits plus ou moins observables ou déductibles. J’essaie de démontrer et de comprendre comment une cosmologie à 6D pourrait radicalement changer notre perception de notre place dans cet univers. Je me demande aussi dans quelle mesure cela ne pourrait pas un jour nous apprendre peut-être le voyage dans le temps et l’espace et comment même la téléportation pourrait être possible à travers la 5e et la 6e dimension. Bien sûr, bien que j’essaie de démontrer ces théories par des choses plus ou moins vérifiables, une grande part de mes théories est au stade de spéculation.
Je vous invite, si vous le souhaitez, à rejoindre la discussion et à partager vos réflexions via le bouton “commenter” ci-dessous. Si vous êtes intéressé par mes recherches, vous pouvez également vous abonner à ma page Facebook ou, mieux encore, accéder à mon livre gratuit et le lire.
Cet article, fruit de longues années de réflexion sur des questions spatiotemporelles, est librement utilisable, à condition de citer la source :
https://dichotomieresolue.jimdofree.com/
Olivier Dusong

